Oberseminar "Mathematik des Maschinellen Lernens und Angewandte Analysis" - M.Sc. Jona Laubmann
Duality of Nonlinear Eigenproblems
| Datum: | 16.04.2025, 14:15 - 15:15 Uhr |
| Kategorie: | Veranstaltung |
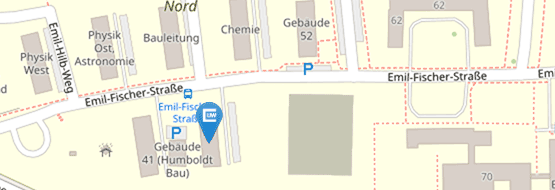
| Ort: | Hubland Nord, Geb. 40, 01.003 |
| Veranstalter: | Institut für Mathematik |
| Vortragende: | M.Sc. Jona Laubmann - Universität Erlangen |
Nonlinear eigenproblems are an interesting tool for image processing and clustering tasks in data science. Recent approaches aim to determine eigenvectors, and in particular ground states, of nonlinear operators via respective energy functionals such as the total variation regularization. Typically, these eigenvectors are numerically approximated using gradient flows to minimize a nonlinear Rayleigh quotient, which is challenging due to the nonconvex and nondifferentiable nature of the problem.
In this talk, we formulate a dual theory for nonlinear eigenvectors based on the Fenchel conjugate in the setting of a broad class of energy functionals on Banach spaces, e.g., the popular p-Dirichlet energy on Sobolev spaces. Within this framework we identify the dual problem as the nonlinear eigenproblem of the inverse operator. In particular, in our formulation the minimization of the nonlinear Rayleigh quotient translates to the maximization of a dual Rayleigh quotient.
We show that the simple inverse power method possesses the ability to maximize the dual Rayleigh quotient and converges to eigenvectors even in our abstract setting with only mild assumptions on the energy functionals. Furthermore, we give an intuitive geometric characterization which connects the primal and dual problem of computing nonlinear eigenvectors. To validate our theoretical results, we perform various numerical experiments for computing nonlinear eigenfunctions.