Schokoladenquadrate - Unterrichtliche Ideen

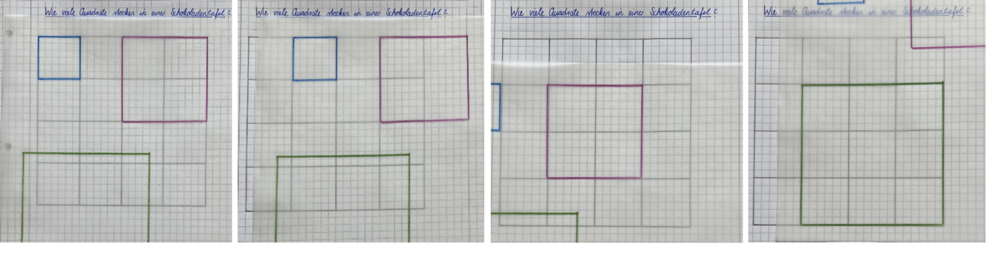
Als Einstieg fungiert die Frage „Wie viele Quadrate stecken in einer kleinen Schokoladentafel?“

Gemeinsam betrachten die Kinder eine 2•2 - Schokoladentafel und nennen die Anzahl der Quadrate, die in dieser Tafel stecken. Einige Kinder werden vermutlich das große 2•2 - Quadrat übersehen. An dieser Stelle wird bereits angebahnt, dass es verschieden große Quadrate gibt und somit fünf Quadrate in der Tafel stecken. Hilfreich ist es hier die Begriffe  1•1 - Quadrat (blau) und 2•2 - Quadrat (pink) einzuführen. Farben für die unterschiedlichen Größen der Quadrate erleichtern die Argumentationen.

Im Anschluss beschäftigen sich die Kinder ausführlich mit einer  4•4 - Schokoladentafel (Forscherkarte 1).

In der Erkundungsphase arbeiten die Kinder zunächst allein, um eine individuelle Auseinandersetzung mit der Aufgabe sowie unterschiedliche Vorgehensweisen zu ermöglichen. Einige Kinder zeichnen evtl. selbstständig auf Karopapier einige 4•4 - Quadrate auf, um die entdeckten kleinen und großen Quadrate einzuzeichnen.

Das Festhalten der möglichen Lösungen erleichtert nicht nur das Auffinden einer gewissen Systematik, sondern ermöglicht auch den Austausch mit anderen in der gemeinsamen Phase.

Als Differenzierung für leistungsschwächere Kinder bietet sich die Betrachtung einer 3•3 – Schokoladentafel an.

Die meisten Kinder entdecken, dass in dieser Schokoladentafel vier verschiedene Größen an Quadraten stecken und finden bereits einige Möglichkeiten. Hierbei handelt es sich um eine einfache Entdeckung, die eine Voraussetzung für das weitere Vorgehen darstellt.

Als Hilfestellung für das Auffinden weiterer bzw. aller Möglichkeiten werden den Kindern verschieden große Quadrate in Papierform (vorzugsweise Transparentpapier) angeboten. Alternativ können sie die Quadrate auf eine Folie aufzeichnen.

So ist es möglich, die Quadrate in ihren unterschiedlichen Größen auch überlappend zu legen bzw. schrittweise zu verschieben. Diese spielerischen Handlungen sind bedeutsam für die Entwicklung einer systematischen Vorgehensweise.

Einigen Schüler:innen fällt bereits hier auf, dass sich das Ergebnis aus Quadratzahlen zusammensetzt:

Es gibt ein   4•4 - Quadrat, vier  3•3 - Quadrate, neun  2•2 - Quadrate und sechszehn  1•1 - Quadrat.

Die Anzahl der Quadrate für eine  4•4 - Schokoladentafel lässt sich somit rechnerisch wie folgt darstellen: 1 + 4 + 9 + 16 = 30.

Die Beschreibung und Begründung (Kompetenz „mathematisch Argumentieren“) einer systematischen Vorgehensweise stellt eine komplexe Anforderung an Grundschulkinder dar. Durch das Legen und Verschieben der farbigen Quadrate gelingt es den Kindern ihre eigene Vorgehensweise zu erklären.

Forscherkarte 2 lenkt den Fokus auf eine  6•6 - Schokoladentafel, wobei die Kinder aufgefordert werden, ihre bisherigen Erkenntnisse zu nutzen.

Die meisten Kinder werden erkennen, dass nun zwei weitere Größen an Quadraten (5•5 - Quadrat und  6•6 - Quadrat) hinzukommen. Nicht allen Kinder wird es jedoch leicht fallen, die bisher erprobten Erfahrungen auf die  6•6 - Schokoladentafel zu übertragen. Hier es es denkbar, den Anspruch für einige Kinder zu reduzieren und alternativ die fehlende 5•5 - Schokoladentafel zu erforschen. Auf diese Weise wird auch die „Lücke“ zwischen den betrachteten Tafeln geschlossen. Die bisherigen Betrachtungen verschiedener Schokoladentafeln legen die Vermutung nahe, dass sich bei allen Schokoladentafeln die Anzahl aller Quadrate aus Quadratzahlen zusammensetzt (vgl. mathematischer Hintergrund).

Forscherkarte 3 fasst nun die Entdeckungen tabellarisch zusammen und ermöglicht die Verallgemeinerung der Erkenntnisse. Spätestens an dieser Stelle wird beim Ausfüllen der Tabelle die „Lücke“ für die fehlenden 3•3 - Schokoladentafel geschlossen.

Eine Ausweitung des Aufgabenformates stellt die Erfindungsphase dar.