Deutsch Intern
Complex Analysis

Kraus, Daniela

PD Dr. Daniela Kraus

Lecturer
Chair of Mathematics IV
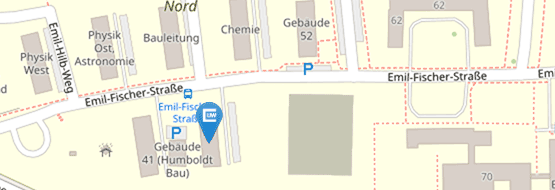
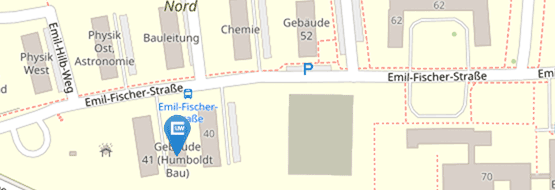
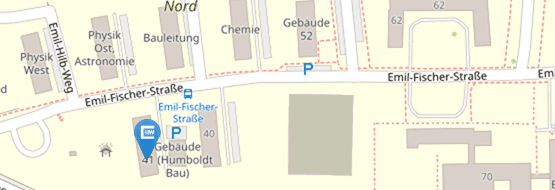
Emil-Fischer-Straße 40
97074 Würzburg
Building: 40 (Mathematik Ost)
Room: 02.008
Phone: +49 931 31-85028
Fax: +49 931 31-85376

 

Sprechstunde: by agreement

 

 

 

Homepage

 

 

  • Weighted distortion in conformal mapping in euclidean, hyperbolic and elliptic geometry
    (with Oliver Roth)
    Ann. Acad. Sci. Fenn. Math. 31, 111-130, 2006.

     

  • A boundary version of Ahlfors' Lemma, locally complete conformal metrics and conformally invariant reflection principles for analytic maps
    (with Oliver Roth and Stephan Ruscheweyh)
    J. d'Analyse Math. 101, 219-256, 2007.

     

  • Critical points of inner functions, nonlinear partial differential equations, and an extension of Liouville's theorem
    (with Oliver Roth)
    J. London Math. Soc. 77, 183-202, 2008.

     

  • The behaviour of solutions of the Gaussian curvature equation near an isolated boundary point
    (with Oliver Roth)
    Math. Proc. Cambridge Phil. Soc. 145, 643-667, 2008.

     

  • Beurling's free boundary value problem in conformal geometry
    (with Florian Bauer, Oliver Roth and Elias Wegert)
    Israel Journal Math. 180, 223-254, 2010

     

  • On the isolated singularities of the solutions of the Gaussian curvature equation for nonnegative curvature
    (with Oliver Roth)
    J. Math. Anal. Appl. 345 No. 2, 628-631, 2008.

     

  • Conformal Metrics
    (with Oliver Roth)
    to appear Lecture Notes Ramanujan Math. Society
    see arXiv:0805.2235

     

  • Metrics with conical singularities on the sphere and sharp extensions of the theorems of Landau and Schottky
    (with Oliver Roth and Toshiyuki Sugawa)
    Math. Z. 267 No. 3-4, 851-868, 2011.

     

  • On Beurling's boundary value problem in Circle Packing
    (with Oliver Roth and Elias Wegert)
    Complex Variables and Elliptic Equations 57 No. 2-4, 397-410, 2012.

     

  • Critical sets of bounded analytic functions, zero sets of Bergman spaces and nonpositive curvature
    Proc. London Math. Soc. 106 No. 4, 931-956, 2013.

     

  • Critical points, the Gauss curvature equation and Blaschke products
    (with Oliver Roth)
    Fields Institute Communications 65, 133-157, 2012.

     

  • Maximal Blaschke products
    (with Oliver Roth)
    Adv. Math. 241, 58-78, 2013.

     

  • Composition and decomposition of indestructible Blaschke products
    (with Oliver Roth)
    to appear Computational Methods and Function Theory